合成抵抗の計算。
中学生で習う理科の中で、ややこしくてつまずきやすいポイントの一つだと思います。
そして大人になっても、電気工事士などの電気系の資格試験には欠かすことのできない、電気の基本的な知識の一つでもあります。
決して難しい計算ではないので慣れれば簡単なのですが、理解するまではなかなか大変です。
そこで今回は、合成抵抗の計算を分かりやすくまとめてみました!
抵抗を直列・並列につないだときのイメージのイラストも載せていますので、ぜひ最後まで読んでみてくださいね(^^)
目次
合成抵抗の概要
それでは、早速ですがまずは抵抗をそれぞれ直列・並列につないだ場合、抵抗がどのように変わるのかの概要をお伝えします。
こちらです。
- 【直列つなぎ】回路全体の抵抗が増える
- 【並列つなぎ】回路全体の抵抗が減る
このように、抵抗を直列につないだ場合は回路全体の抵抗は増えて、並列につないだ場合は回路全体の抵抗は減ります。
以降の章では、合成抵抗のイメージや実際の計算方法について、さらに詳しくお伝えしていきます。
合成抵抗のイメージ
合成抵抗の計算、いきなり計算式だけ見てもなかなかイメージが湧きづらいかと思いますので、まずは抵抗そのものと、それをつなげた合成抵抗のイメージからお伝えしていきたいと思います。
抵抗のイメージ
まずは、ひとつの単体の抵抗のイメージです。
こちらです。
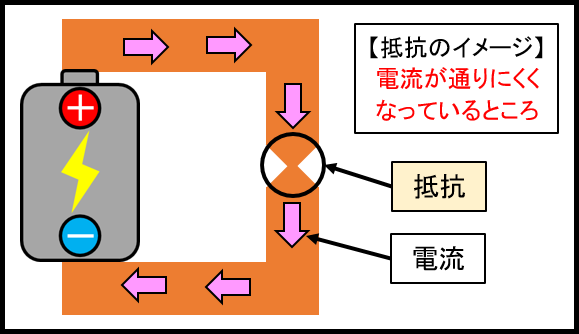
このように、抵抗は電流が通りにくくなっている部分といったイメージなります。
そして、抵抗の数値が高ければ高いほど、より電流が流れにくくなります。
直列の合成抵抗のイメージ
抵抗単体のイメージが湧きましたので、次は直列の合成抵抗のイメージです。
こちらです。

抵抗を直列につなぐと、電流が流れにくい部分が増えるので、どんどん電流が流れにくくなっていきます。
これは、回路全体では抵抗の数値が増えることを意味しています。
並列の合成抵抗のイメージ
次は、抵抗を並列につないだ場合のイメージです。
こちらです。
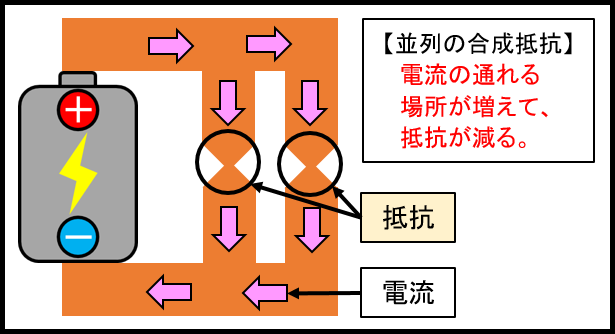
抵抗を並列につなぐと、電流の通り道が増えることになるので、電流はどんどん流れやすくなります。
これは、回路全体では抵抗の数値が減ることを意味しています。
合成抵抗の計算方法
ここからは、いよいよ合成抵抗の計算方法をお伝えしていきます。
数式なども出てきてちょっと難しくなりますが、がんばってついてきてくださいね。
直列つなぎの計算方法
まずは、直列つなぎの計算方法です。
直列つなぎの合成抵抗の公式は、こちらになります。
直列つなぎの公式!
$$R=R_1+R_2+{\cdot}{\cdot}{\cdot}+R_n$$
このように、直列つなぎの合成抵抗の求め方はとても簡単で、ただ単純にその数値を足せばOKです。
イラストにすると、このような感じです。
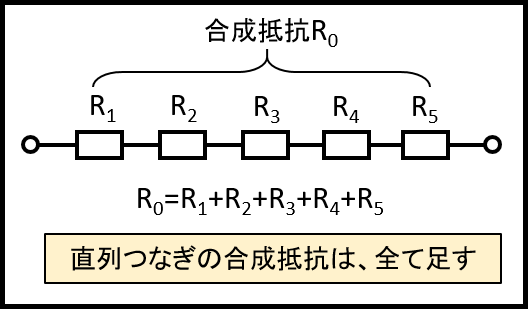
直列の場合は、計算はとっても簡単ですね!
並列つなぎの計算方法
次は、並列つなぎの計算方法です。
並列つなぎの合成抵抗の公式は、こちらになります。
並列つなぎの公式!
$$\frac{1}{R_0}=\frac{1}{R_1}+\frac{1}{R_2}+{\cdot}{\cdot}{\cdot}+\frac{1}{R_n}$$
このように、並列つなぎの合成抵抗を求め方は、その逆数を足し算します。
合成抵抗の方も逆数になっているので、その点も注意が必要です。
イラストにすると、このような感じです。
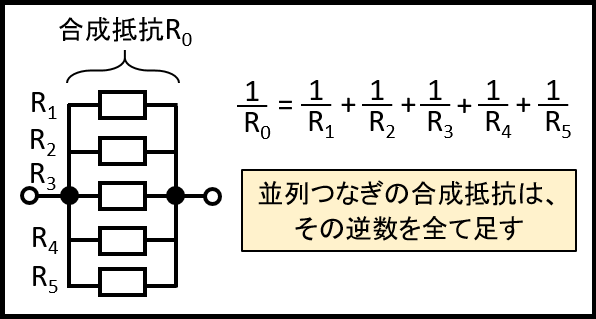
並列の合成抵抗の計算は、分数になるので直列と比べるとちょっと難しいですね。
また、抵抗の並列つなぎで、抵抗の数が2個のときのみ「和分の積」というこちらの公式が使えます。
和分の積
$$R_0=\frac{R_1R_2}{R_1+R_2}$$
抵抗の逆数である1/Rは、「コンダクタンス」と呼ばれており、これは電気の流れやすさを表しています。数値が大きいほど、電流が流れやすいことを意味しています。
並列つなぎの公式では、このコンダクタンスがどんどん足されていますので、足せば足すほど電気が流れやすくなるということになります。
合成抵抗の例題
ここまで、合成抵抗の計算方法についていろいろと学んできましたので、最後の章では実際に例題を解いてみたいと思います!
直列つなぎ
まずは、直列つなぎの問題です。
こちらの抵抗の、合成抵抗を計算してみましょう。
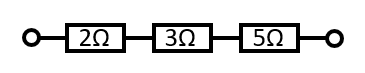
直列の場合はただ全部足せば良いだけですので、解答はこちらになります。
$$R=2+3+5=10(Ω)$$
単純な足し算なので、すぐに計算できますね。
並列つなぎ
次は、並列つなぎの問題です。
こちらの抵抗の、合成抵抗を計算してみましょう。
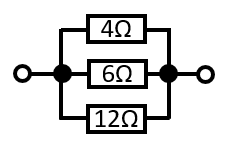
並列の場合は逆数の足し算になりますから、解答はこちらになります。
$$\begin{eqnarray}\frac{1}{R}&=&\frac{1}{4}+\frac{1}{6}+\frac{1}{12}\\&=&\frac{3}{12}+\frac{2}{12}+\frac{1}{12}\\&=&\frac{6}{12}\\&=&\frac{1}{2}\end{eqnarray}$$
$$R=2(Ω)$$
このように並列つなぎの計算では分数の計算方法が必須になりますので、小学生のときにならった分数の計算方法を思い出しながら解いていきたいですね。
両方あるとき
最後は、直列と並列が両方ある場合の問題です。
こちらの抵抗の、合成抵抗を計算してみましょう。
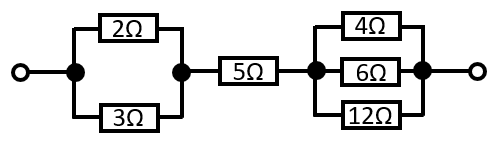
このような場合は、まずは並列の部分の部分的な合成抵抗から計算します。
これは、下記の通り、抵抗をRa・Rb・Rcの3つの部分に分けて考えるというイメージです。
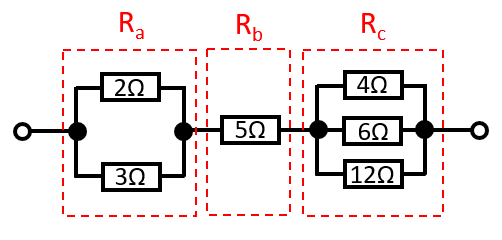
そして、実際に計算した値がこちらです。
◆Raの抵抗値
$$\frac{1}{R_a}=\frac{1}{2}+\frac{1}{3}=\frac{3}{6}+\frac{2}{6}=\frac{5}{6}$$
$$R_a=\frac{6}{5}=1.2(Ω)$$
また、和分の積の公式を使うと、このようにも計算できます。
$$R_a=\frac{2\cdot3}{2+3}=\frac{6}{5}=1.2(Ω)$$
◆Rbの抵抗値
これは、ひとつなのでそのまま5Ωになります。
◆Rcの抵抗値
これは、並列の例題と同じ数値ですね。
そのため、抵抗の数値は2Ωになります。
◆合成抵抗の数値
これで、Ra・Rb・Rcの数値が分かりましたので、この回路はこの3つの抵抗の直列つなぎと考えることができます。
そのため、この合成抵抗の解答はこちらになります。
$$\begin{eqnarray}R&=&R_a+R_b+R_c\\&=&1.2+5+2\\&=&8.2(Ω)\end{eqnarray}$$
直列と並列が両方あると一見複雑なように見えますが、基本的な考え方は片方のときと同じですので、慣れたらそんなに難しくはないですよ。
まとめ
以上で、合成抵抗の計算方法についての話を終わります。
まとめると、下記の通りです。
- 抵抗を直列につなぐと、抵抗値が上がる
- 抵抗を並列につなぐと、抵抗値が下がる
- 直列つなぎの合成抵抗は、その数値を全部足す
- 並列つなぎの合成抵抗は、その逆数を全部足す
- 抵抗が2個のときの並列つなぎでは「和分の積」という公式が使える
- 直列と並列が混ざった回路では、まず並列の部分から計算する
合成抵抗の計算の仕方、お分かり頂けましたでしょうか?
最初はとっつきにく部分がありますが、計算自体は小学生でもできるレベルなので決して難しいことではありません。
正しく理解して、学校のテストや資格試験などの問題を乗り切っていきたいですね(^^)
※乾電池と豆電球の直列つなぎと並列つなぎについても別ページで詳しくお話していますので、興味のある方はこちらにも遊びにきてくださいね。
編集した本が出版されました!
◆キャリアの話をしよう◆

こちらは、現役管理職ワーママ(部長職)のあづさんが著者の本です。あづさんがインタビューをするという形で、合計4名の女性の方に、ご自身のキャリアをお話しして頂いています。
ここまで等身大のキャリアの話は他では知ることができないと思いますので、キャリアでお悩みの女性の方はぜひ読んでみてください。
◆とろけて香る茄子麻辣のおいしい秘密◆

こちらは、ナス農家をされているハーティッチファーム代表の賀川元史さんが著者の本です。著者さんご自身が開発された日本初の麻婆茄子の瓶詰め「とろけて香る茄子麻辣」の開発秘話です。
いかにして日本初の商品が作られていったのかをストーリー形式でお話ししていますので、ナス好きの方はぜひ読まれてみてください。
























コメントを残す