実効値。
交流電源に、どのくらいの電圧が掛かっているかを表すための数値です。
仕事や勉強で電気に関わっていると必ず出てくる言葉なので、何となくは知っている方も多いと思います。
しかし、いざどんなものかと聞かれると、意外とはっきり答えられないのもこの実効値です。
そこで今回は、交流の実効値とはどのようなものなのか分かりやすくまとめてみました！
合わせて、平均値との違いや求め方についても一緒にお話していますので、ぜひ最後まで読んでみてくださいね(^^)
交流の実効値
それでは、早速ですが交流の実効値の定義からお伝えしたいと思います。
こちらです。
ある電気抵抗に交流電圧を１周期加えた時の電力と、同じ抵抗に直流電圧を加えた時の電力が互いに等しくなるとき、交流電圧の実効値はその直流電圧と同じ値とする。
定義はこのようになっているのですが、文章だけではなかなか理解するのが難しいですね。
そこでこれをイラストにしてみると、このようになります。
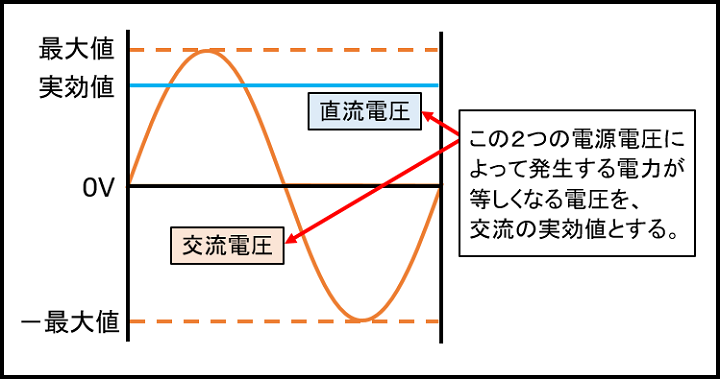
交流電源の電圧はイラストの通り波の形をしていて、電圧が常に変化しています。
そうすると電力も電圧の変化と一緒に変化するので常に変ります。
そんな交流電圧によって発生する電力を１周期分（波１つ分）足した時の電力が、直流電圧によって発生した電力と同じのなるとき、その電圧のことを実効値と呼んでいるのです。
そして先に結果から言いますと、交流電源の最大電圧をVm、実効値をVeとすると、この２つには下記のような関係があります。
$$V_e=\frac{V_m}{\sqrt{2}}$$
このように、交流の実効値は最大値のルート２分の１倍になります。
また、実効値を基準とすると、下記のように書き換えることもできます。
$$V_m=\sqrt{2}V_e$$
これは、実効値のルート２倍が、その交流電源の最大電圧になることを示しています。
ここまでで、ざっくりと交流の実効値を理解することができました！
そして次の章からは、実効値の身近な例や、最大電圧と実効値がなぜそのような関係になるのかについて更に深掘りしていきます。
実効値の例
第１章で実効値とはどのようなものなのかが分かりましたので、ここでは身近な実効値の例と見てみようと思います。
私たちの一番身近にある交流と言えば、そう、おうちのコンセントにも来ている商用電源ですよね。
この商用電源は交流で家庭に届いており、交流なのでここにももちろん実効値があります。
そして、商用電源の電圧をグラフにしたのがこちらです。
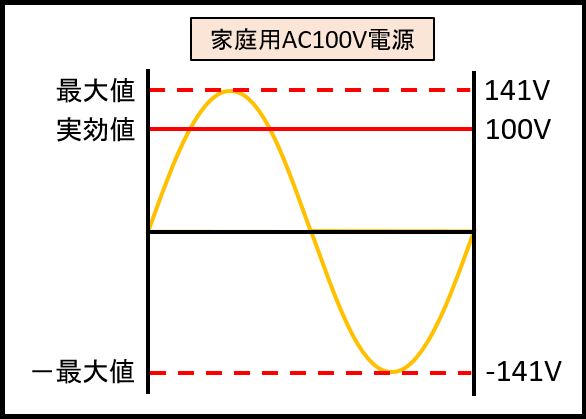
そうなのです。
おうちに来ている電源は100Vというのはみんな知っている常識だと思いますが、この100Vというのは交流の実効値のことだったのですね。
このようにこの100Vは実効値のため、最大値はそのルート２倍になります。
ルート２の数値は「1.414213…」なので、おうちに来ている100Vの交流電源は、瞬間的に141Vの電圧が掛かっていることになります。
※商用の交流電源については別ページで詳しくお話していますので、興味のある方はこちらにも遊びにきてくださいね。
最大値と実効値の関係
ここからは少し難しくはなってしまいますが、最大値と実効値の関係を数式とグラフを使って探っていきたいと思います。
先ほどは電圧のグラフでしたが、実効値は電力との関係が深いので、まずは電力のグラフを作ってみたいと思います。
ここで、
- 最大電圧＝Vm
- 実効値＝Ve
- 抵抗値＝R
- 実効値の直流電力＝PDC
- 最大電圧Vmの交流電力＝PAC
- 角周波数＝ω
- 時刻＝t
とおくと、PDCとPACは、それぞれ下記のような式で表すことができます。
$$P_{DC}=V_e{\cdot}I=\frac{V_e^2}{R}$$
$$P_{AC}=V_m{\rm sin}{\omega}t{\cdot}I=\frac{V_m^2{\rm sin}^2{\omega}t}{R}$$
※電力の計算方法は別ページで詳しくお話していますので、興味のある方はこちらにも遊びにきてくださいね。
この式をグラフにしてみると、このようになります。
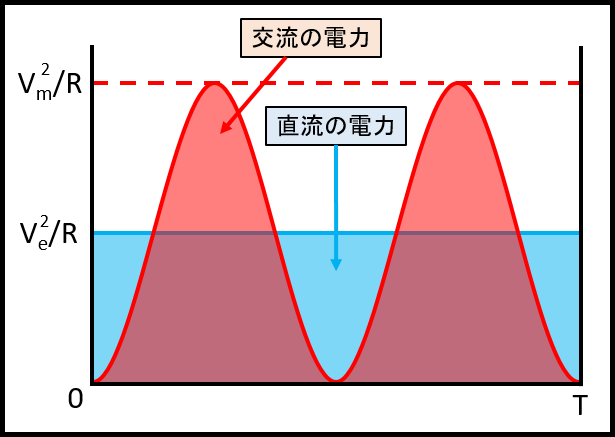
この時、交流１周期（=T）分の電力は、直流は青色の部分の面積、交流は赤色の部分の面積になります。
ここで実効値の定義を思い出してみると、直流と交流の電力が同じ電圧になるものを実効値とするとありましたので、先ほどのイラストで言うと青色の部分と赤色の部分の面積が同じでなければならないということを意味しています。
そこで、面積計算といえば積分の出番です。
実際に、青色の部分と赤色の部分の面積を計算してみたいと思います。
実効値Veの直流の電力
まずは、青色の部分の面積、実効値Veの直流の積算電力(=SDC)を計算します。
先ほど出てきた電力の式を、交流１周期分(=T)の時間で積分をしてみます。
$$\begin{eqnarray}{S_{DC}}&=&\int_0^T\frac{V_e^2}{R}dt\\&=&\frac{V_e^2}{R}\int_0^Tdt\\&=&\frac{V_e^2}{R}\left[t\right]_0^T\\&=&\frac{V_e^2}{R}(T-0)\\&=&\frac{TV_e^2}{R}\end{eqnarray}$$
これが、実効値Veの直流の、時間Tまで積算電力になります。
最大値Vmの交流の電力
次は、赤色の部分の面積、最大電圧Vmの交流の積算電力(=SAC)を計算します。
こちらも、先ほど出てきた電力の式を、交流１周期分(=T)の時間で積分をしてみます。
$$\begin{eqnarray}{S_{AC}}&=&\int_0^T\frac{V_m^2{\rm sin}^2{\omega}t}{R}dt\\&=&\frac{V_m^2}{R}\int_0^T{\rm sin}^2{\omega}tdt\\&=&\frac{V_m^2}{R}\left[\frac{t}{2}-\frac{{\rm sin}2{\omega}t}{4{\omega}}\right]_0^T\\&=&\frac{V_m^2}{R}\left(\frac{T}{2}-0\right)\\&=&\frac{TV_m^2}{2R}\end{eqnarray}$$
これが、最大電圧Vmの交流の電力の、時間Tまで積算電力になります。
VmとVeの関係式
これで、直流と交流の２つの時間Tまでの積算電力が計算できました。
そして交流の実効値ではこの２つが同じにならなければならないので、この２つをイコールで結んで、VmとVeの関係式に直してみます。
$$\begin{eqnarray}S_{DC}&=&S_{AC}\\\frac{TV_e^2}{R}&=&\frac{TV_m^2}{2R}\\V_e^2&=&\frac{V_m^2}{2}\\V_e&=&\frac{V_m}{\sqrt{2}}\end{eqnarray}$$
そうすると、実効値Veは最大電圧Vmのルート２分の１倍という結果が導かれます。
第１章ではこの結果だけ述べましたが、これでなぜその値になるのかスッキリと分かることができました(^^)
交流の平均値
最後に、交流の平均値についてお伝えします。
これまでお話した実効値は電力の平均でしたが、平均値はまさに、電圧の平均値のことになります。
といっても、交流では電圧がプラスとマイナスを行き来してそのまま平均すると０になってしまうので、平均値はその絶対値の平均を取ります。
グラフにすると、このような感じです。
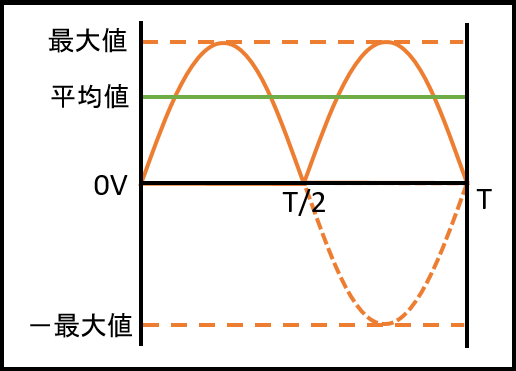
そしてここでも、実際に計算してみたいと思います。
グラフを見ると、交流の絶対値は波長の半分の山がずっと繰り返している形になっていますので、半波長である時刻T/2までの積算電圧を求めて、その平均値（＝Va）を出してみます。
$$\begin{eqnarray}V_a&=&\frac{1}{\frac{T}{2}}\int_0^{\frac{T}{2}}V_m{\rm sin}{\omega}tdt\\&=&\frac{2V_m}{T}\int_0^{\frac{T}{2}}{\rm sin}{\omega}tdt\\&=&\frac{2V_m}{T}{\cdot}-\frac{1}{{\omega}}\left[{\rm cos}{\omega}t\right]_0^{\frac{T}{2}}\\&=&\frac{2V_m}{T}{\cdot}-\frac{T}{2{\pi}}(-1-1)\\&=&\frac{2V_m}{\pi}\end{eqnarray}$$
平均値は、以上のような形になりました。
また、実効値を基準にすると下記のようにも書くことができますね。
$$V_a=\frac{2\sqrt{2}V_e}{{\pi}}$$
平均値が分かったので、ちょっと実効値とどちらが大きいかも確認しておきたいと思います。
$$実効値V_e＝\frac{V_m}{\sqrt{2}}\approx0.707V_m$$
$$平均値V_a=\frac{2V_m}{\pi}\approx0.637V_m$$
このように、実効値と平均値の値を比較すると、実効値の値の方が少しだけ高くなります。
まとめ
以上で、交流の実効値と、その求め方や平均値との違いについての話を終わります。
まとめると、下記の通りです。
- 実効値は、電力の平均になっている
- 実効値は、最大電圧のルート２分の１倍
- 実効値の身近な例は、家庭用100V電源
- 家庭用100V電源の100Vは、実効値のことを表している
- 家庭用100V電源の最大電圧は、141Vになる
- 平均値は、電圧の平均になっている
- 実効値と平均値を比べると、実効値の方が少し高い
今まで何となくの理解だった実効値ですが、これでスッキリはっきり理解することができました(^^)
家庭用電源を始めとして、この実効値は電気の世界では本当に良くでてきますから、正しく理解して電気についての知識を深めていきたいですね！
編集した本が出版されました！
この度、私(星野なゆた)が編集として入らせて頂いたKindle本「食べたい！がとまらない とろけて香る茄子麻辣のおいしい秘密:日本初！常温保存できる瓶詰め麻婆茄子商品開発ストーリー（賀川元史著）が出版されました！
すでに読んでくださった方からは大好評を頂いています。ナスが好きな方は、ぜひ読んでいただけたら嬉しいです(^^)
コメントを残す