ニュートン(N)。
国際単位系の中で、力の強さを表す単位です。
しかしこのニュートンという単位、日常生活ではほとんど登場しないので、どんな単位なのかあまりピンと来ないところ、ありますよね。
そこで今回は、ニュートンという単位がどのようなものなのか徹底的にまとめてみました！
合わせて、工学の世界で良く使われている単位であるキログラム重（kgf）の定義・Nとkgfの換算方法・運動方程式と力の関係・ニュートンという単位の名前の由来についてもお話していますので、ぜひ最後まで読んでみてくださいね(^^)
1ニュートン(N)の定義
それでは、早速ですが1ニュートン(N)の定義からお伝えします。
こちらです。
1kgの質量を持つ物体に、1m/s2の加速度を生じさせる力
言葉では若干分かりづらいですので、図にするとこうなります。
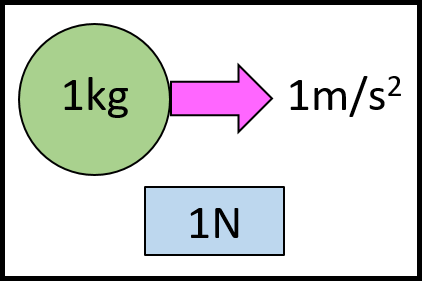
質量1kgの物体に1m/s2の加速度を与えるのに必要な力が1Nだったのですね。
※力の単位の定義にもなっている質量と加速度の定義については別ページで詳しくお話していますので、興味のある方はこちらにも遊びにきてくださいね。
ただ、これで定義は分かりましたが、じゃあ実際にどのくらいの力なのかはまだ良く分からないですよね。
そこで実感できる1Nのちからの強さは、良く次のように言われています。
100gの物体を持った時に感じる力
この表現であれば、どのくらいの力なのかとても良く分かりますよね！
身近なもので100gのものと言えば果物のみかんがそのくらいの重さですので、1Nはみかんを持った時に感じるくらいの重さです。
みかんを重たいと思うことはまずありませんから、100gの物体を持った時に感じる力が1Nであるのであれば、1Nの力はそんなに強くないですね。
しかしここで、なぜ1Nの力は100gの物体を持った時に感じる力になるのかという、新たな疑問も出てきます。
それを理解するにはもう一つの力の単位であるキログラム重(kgf)も知る必要が出てきますので、次の章からキログラム重についても見ていきたいと思います。
1キログラム重(kgf)の定義
ここからは、もう一つの力の単位であるキログラム重(kgf)の定義を見ていきます。
kgfは国際単位系にはなっていませんが、Nよりも感覚的に分かりやすいので、工学の世界では今でも好んで使われる単位です。
そして、1キログラム重(kgf)の定義は下記の通りです。
1kgの質量を持つ物体にかかる重力の大きさ
さきほどのニュートンの定義とよく似ていますが、加速度の部分が重力に変わっていますね。
でも、実は重力というのも加速度なので、同じ定義の仕方になっているのです。
そして違うのは、その加速度の値だけです。
1Nは1m/s2の加速度を与える力ですが、重力の加速度は9.81m/s2なので、1kgfは1kgの物体に9.81m/s2の加速度を与える力ということになります。
図にすると、このような感じです。
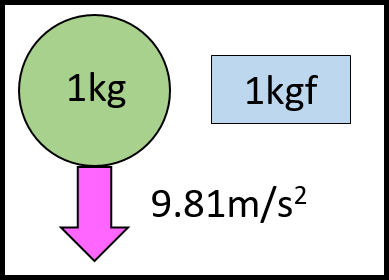
こちらの力の単位は、とても分かりやすいですよね。
重力で発生する力がまさにそれになりますから、1kgfは1kgの物を持った時に感じる力になります。
1kgの物体を持った時に感じる力
これで、ニュートンとキログラム重という２つの力の単位が理解できました！
Nとkfgの換算式
この章では、ニュートンとキログラム重の換算方法をお話します。
前章でお話した定義を見てみると、換算する方法はすぐに分かりますよね。
二つの違いは1kgの物体に与える加速度の違いだけなので、換算式は下記の通りになります。
Nとkgfの換算式
- 1N≒0.102kgf（1÷9.81）
- 1kgf＝9.81N
このように、N→kgfの換算では9.81で割れば、kgf→Nの換算では9.81を掛ければ良いということです。
特にややこしい計算もありませんから、分かればとても簡単ですね！
そして、この換算式が分かれば、第一章で生まれた疑問の、1Nの力の目安がなぜ100gの重さを持った時に感じる力なのかが分かります。
1Nをkgfに換算すると「約0.1kgf＝100gの物体にかかる重力の大きさ」となりますから、100gの物体を持った時に感じる力が1Nの目安と言われているのですね。
また、下記にそれぞれの力の換算するための計算フォームを作りましたので、いろいろと計算して遊んでみてください。
運動方程式と力
これまで、力の単位「N」と「kgf」についてお話しましたが、そもそも力とは何かについても少し触れてみようと思います。
力の定義は、この単位の名前にもなっている物理学者「アイザック・ニュートン」によってまとめられた、運動の３つの法則の中で初めて行われました。
ちなみに、運動の３法則は下記の通りです。
運動の３法則
- 慣性の法則（運動の第１法則）
- 運動の法則（運動の第２法則）
- 作用・反作用の法則（運動の第３法則）
この中の、「運動の法則（運動の第２法則）」のところで力の定義が登場します。
そこで、運動の法則をもう少し詳しくみていくと、このような法則となっています。
質量mの質点の加速度をaとし、作用するすべての力の和をFとすると、aはFに比例し、mに反比例して、a=F/mとなる。
言葉だけだと少し分かりにくいので、イラストにするとこのようになります。
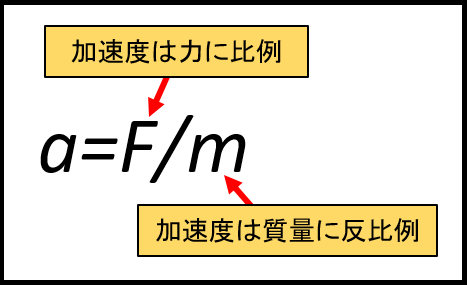
また、この式を変形するとF=maとなり、力は質量と加速度に比例すると言い換えることもできます。
物理の教科書などではこの形の式で出てくることが多いので、こちらの式の方が分かりやすいですかね。
このように力は質量×加速度という定義になるので、単位の次元はkg・m/s2になります。
また、この式は慣性の法則とも密接に関係しており、加速度aが質量mに反比例するということは、「重たい物ほど動きを変えづらい」ということを意味しています。
良く交通安全の標語で「車は急に止まれない」というのがありますが、これは車はとても重たいので、止めるためには大きい力が必要でちょっとやそっとで止まることができないからだったのですね。
単位の名前の由来
最後はちょっと余談になりますが、力の単位の名前が「ニュートン」になった由来についてお話したいと思います。
もうお察しかもしれませんが、単位の由来はかの有名な物理学者「アイザック・ニュートン」です。17世紀ごろにイギリスで大活躍し、重力や微積分を発見した最も有名な物理学者のうちの一人ですね。
そんなニュートンの数々の功績の栄誉を称えて、1948年に国際単位系（SI単位）の力の単位を「ニュートン」という名前にすることが決まりました。
一見すると、人物の名前を単位にするなんてちょっと不思議な感じがしますが、実は普段私たちが日常で使っている単位にも、人物が由来のものがたくさんあります。
例を挙げると、下記の表のような単位がそうです。
| 単位名 | 記号 | 意味 | 由来の人物 |
|---|---|---|---|
| ニュートン | N | 力 | アイザック・ニュートン |
| パスカル | Pa | 圧力 | ブレーズ・パスカル |
| アンペア | A | 電流 | アンドレ＝マリ・アンペール |
| ボルト | V | 電圧 | アレッサンドロ・ボルタ |
| ワット | W | 電力 | ジェームズ・ワット |
| オーム | Ω | 電気抵抗 | ゲオルク・オーム |
| ヘルツ | Hz | 周波数 | ハインリヒ・ヘルツ |
| 摂氏（セルシウス度） | ℃ | 温度 | アンデルス・セルシウス |
天気予報で出てくる圧力の単位である「パスカル」や、電気製品を買うときによく見かける電力の単位である「ワット」も、実は有名な物理学者の名前が由来になっていたのです。
このうち、なぜか「ニュートン」だけ異常に違和感を感じてしまうのは、他の単位は日常生活で深く馴染んでいるものの物理学者の名前といったイメージは無いですが、ニュートンの場合は単位としてのイメージはほとんどないのに、「木からりんごを落ちるのを見て重力を発見したニュートン」というイメージが強烈に私たちの中にありますので、それが原因なのかもしれませんね。
まとめ
以上で、力の単位「ニュートン(N)」と、それにまつわる関連話についての話を終わります。
まとめると、下記の通りです。
- 1Nの定義＝1kgの物体に1m/s2の加速度を与える力
- 1Nの目安は、100gの物体を持った時に感じる力
- 1kgfの定義＝1kgの物体に重力が掛かったときの力
- 1kgf＝9.81N（重力加速度が9.81m/s2のため）
- N→kgfの換算は、9.81で割る
- kgf→Nの換算は、9.81を掛ける
- 力は、運動の法則の中でF=maと定義されている
今まで、中学の理科でいきなり出てきたのは良いけれど、いまいちピンと来なかった力の単位である「ニュートン」なのですが、一度分かってしまったら全然難しいものではなかったですね！
これからはニュートンという単位に悩むことなく、学校の勉強や大学の研究、仕事の中などでガンガン使っていきたいですね(^^)
編集した本が出版されました！
この度、私(星野なゆた)が編集として入らせて頂いたKindle本「食べたい！がとまらない とろけて香る茄子麻辣のおいしい秘密:日本初！常温保存できる瓶詰め麻婆茄子商品開発ストーリー（賀川元史著）が出版されました！
すでに読んでくださった方からは大好評を頂いています。ナスが好きな方は、ぜひ読んでいただけたら嬉しいです(^^)
コメントを残す